What Is The Instantaneous Rate Of Change At X=2 Of The Function F Given By

The boilerplate rate of change represents the total change in ane variable in relation to the total change of some other variable. Instantaneous rate of change, or derivative, measures the specific rate of change of 1 variable in relation to a specific, infinitesimally small alter in the other variable. The average rate of change of a part can be determined with secant lines and the instantaneous rate of change can exist adamant with tangent lines. As yous will larn, these rates can also be determined using a special blazon of math called calculus.

What is the rate of modify?

Rate of modify is the alter in i variable in relation to the modify in some other variable. A common rate of modify is speed, which measures the change in altitude travelled in relation to the time elapsed. Olympic Gold Medalist, Usain Commodities, became the world's fastest human being running at a top speed of 44.72 km/hr during the 100-meter nuance. On average, his speed was a bit slower (nonetheless, very impressive) at 37.58 km/hr. Bolt's pinnacle speed is an example of an instantaneous rate of change, and his average speed is an average rate of change.

Average Rate of Change

Secant lines are found by connecting 2 points on a curve. The slope of the secant line between two points represents the average rate of change in that interval.

Formula:

Average Charge per unit of Change = Slope(m) = △y/△x = $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ = $\frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}$

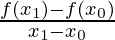
How to find the average rate of modify between two points using a secant line:

Step 1: Describe a secant line connecting the two points.

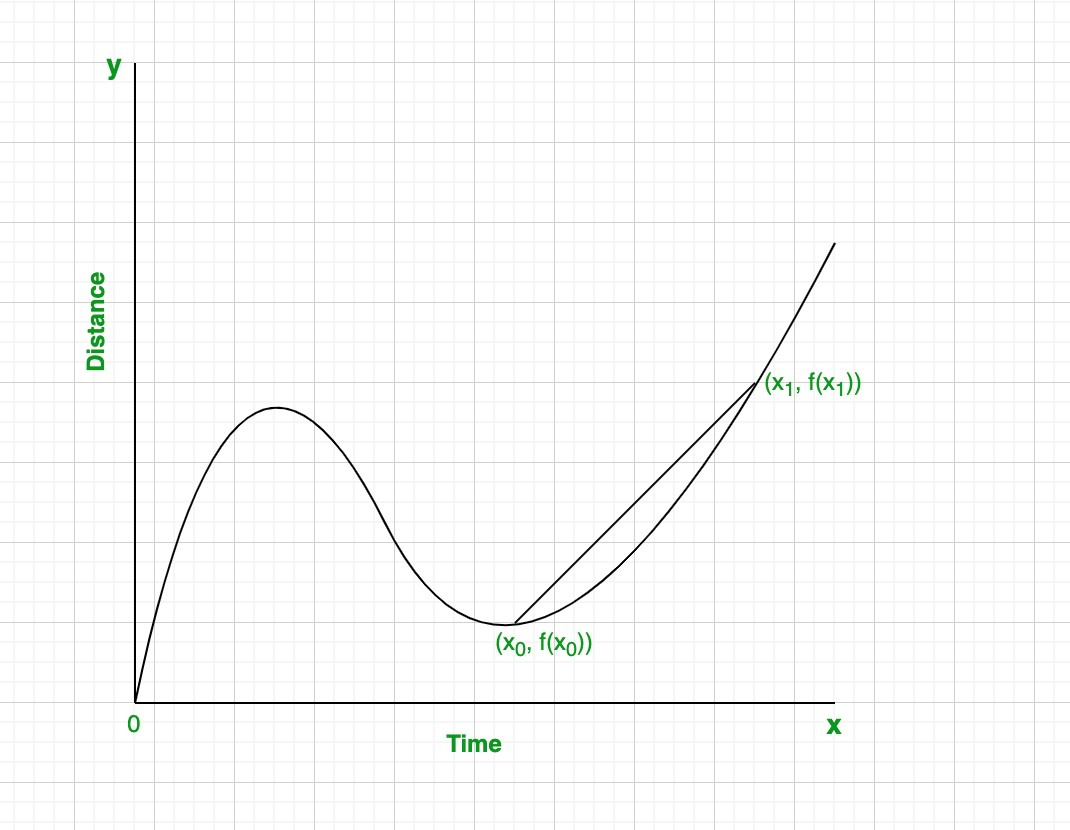
Footstep 2: Utilise the coordinates of the two points to summate the slope.

Equation of slope:
Slope =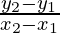 $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

The average change of the function over the given time interval[x₀, ten₁]
Slope =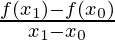 $\frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}$

The slope of the secant line represents the average
rate of modify of the graph in that interval.

One time you've calculated the slope of the secant line, you lot use the slope can write an equation to represent it.

For Example:
Equation of slope:
y – y₀ = m(x – x₀)

thou = gradient of secant line = 4/7
x₀ = 2
y₀ = 9
$y - 9 = \frac{4}{7}(x -2)$

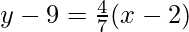
Hence, the equation of the secant line betwixt ten = two and x = 9 is
y – 9 =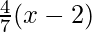 $\frac{4}{7}(x -2)$

Derivatives (Instantaneous Charge per unit of Change)

The tangent line at a bespeak is found by cartoon a straight line that touches a curve at that indicate without crossing over the bend. In other words, the line should locally bear on only one bespeak. The gradient of the tangent line at a indicate represents the instantaneous rate of change, or derivative, at that point.

Formula:

Instantaneous Charge per unit of Change = $f'(x_0) = \lim_{(x_0 \to x_1)} \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}=\lim_{\triangle x \to 0} \frac{f(x_{0}-\triangle x) - f(x_{0})}{\triangle x}$

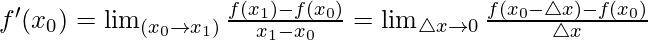
How to discover the derivative at a bespeak using a tangent line:

Step 1: Draw a tangent line at the bespeak.

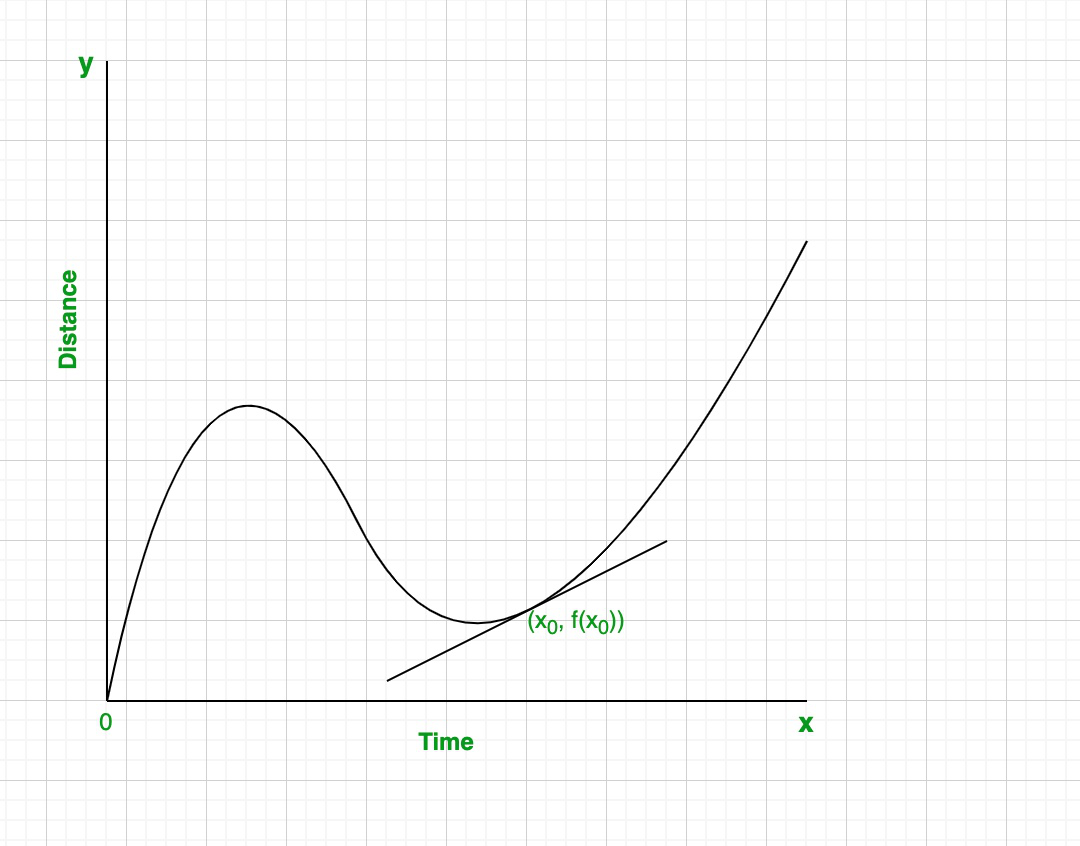
Footstep 2: Use the coordinates of whatsoever two points on that line to calculate the gradient.

Equation of gradient:
Slope =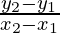 $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

The average change of the function over the given fourth dimension interval x₀
Slope =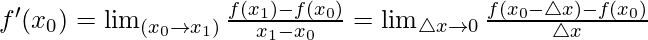 $f'(x_0) = \lim_{(x_0 \to x_1)} \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}=\lim_{\triangle x \to 0} \frac{f(x_{0}-\triangle x) - f(x_{0})}{\triangle x}$

The slope of the tangent line at a bespeak represents
the instantaneous rate of change, or derivative, at that betoken.

One time you've calculated the gradient of the tangent line, you can write an equation to stand for it.

For Example: Equation of slope:
y – y₀ = m(ten – x₀)

g = slope of tangent line = $\frac{5}{6}$
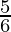
ten₀ = 16
y₀ = half dozen
$y - 16 = \frac{5}{6}(x - 6)$

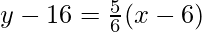
Hence, the equation of the tangent line at x = sixteen is
y – sixteen = \frac{v}{6}(ten – 6)

Derivative Notation

In the early 18th century, there was controversy between the great mathematicians Isaac Newton and Gottfried Wilhelm Leibniz over who the first invent calculus. This argument became known as Prioritätsstreit, or "priority dispute" in German. The disagreement has had lasting touch on the mathematical world, leaving us with two standard derivative notations. Lagrange notation is another common derivative notation, established by French mathematician and philosopher, Joseph-Louis Lagrange.

If nosotros have the role y = f(x), So

1. Leibniz notation:

"Showtime derivative of y with respect to x"
⇒ $\frac{dy}{dx}$

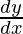
"2nd derivative of y with respect to 10"
⇒ $\frac{dy^2}{d^2x}$

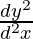
"Offset derivative of y with respect to x
at 10 = 2″
⇒ $\frac{dy}{dx}|_{x=2}$

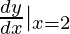
two. Newton notation:

The number of dots above the function
variable represents how many times the
function has been differentiated.
"Get-go derivative of y"
⇒ $\dot y$
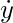
"Second derivative of y"
⇒ $\ddot y$
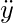
"Beginning derivative of y at x = 2"
⇒ $\dot y (2)$

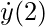
iii. Lagrange notation:

The number of apostrophes after the role
variable represents how many times the
office has been differentiated.
"Commencement derivative of y"
⇒y'
"Commencement derivative of y at x = 2"
⇒y'(two)
"2nd derivative of y"
⇒y"

4. Euler'southward notation

"First derivative"
⇒ D_xf
"Second derivative"
⇒ D_x ⁱⁱf
Here, D represents the differential operator

Sample Problems

Question 1. Find the boilerplate rate of modify over the interval 10 = 4, x = 6.

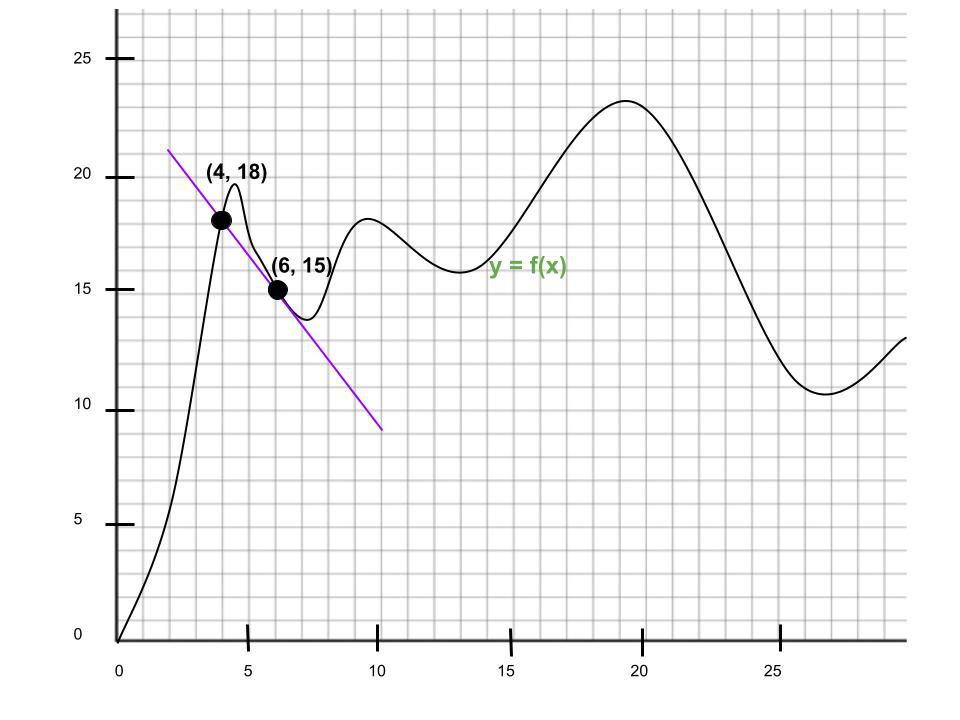
Solution:

Bespeak 1: (4, xviii)

Bespeak 2: (half-dozen, 15)

Gradient = $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

= $\frac{15 - 18}{6-4}$

= $-\frac{3}{2}$

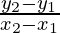
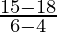
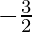
Hence, the average charge per unit of modify = $- \frac{3}{2}$

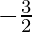
Question 2. Write the equation of the tangent line at x = sixteen.

Solution:

Point of intersection: (16, 18)

Gradient = $\frac{23 - 18}{18 - 16}$

= $\frac{5}{2}$

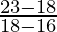
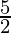
Equation of tangent line:

$y - 18 = \frac {5}{2}(x - 16)$

Question 3. What is the derivative of the graph at x = xx? Express your reply in Leibniz notation.

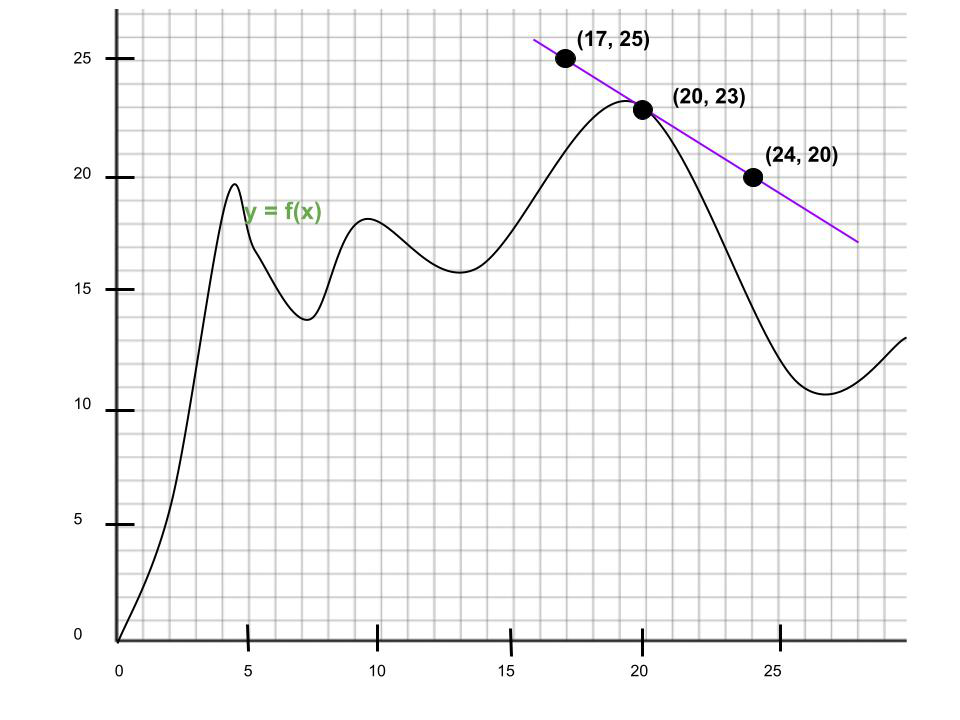
Solution:

Given indicate of intersection: (20, 23)

Slope of tangent line = $\frac{20-25}{20-17}$

= $-\frac{5}{3}$

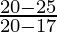
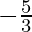
So, the Leibniz notation: $\frac {dy}{dx} | _{x=20} = -\frac{5}{3}$

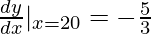
Question four. Observe the derivative of the graph at x = 4. Express your answer in Newton'southward notation.

Solution:

Given indicate of intersection: (4, 18)

Slope of tangent line = $\frac{25 - 18}{7-4}$ = $\frac{7}{3}$

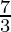
And then, the Newton's notation $\dot y(4) = \frac{7}{3}$

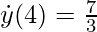
Question 5. Find the average rate of alter over the interval x = iv, 10 = 25. How does this compare to the derivative at 10 = 4?

Solution:

Gradient of secant line = $\frac {12 - 18}{25-4}$

= $- \frac{6}{21}$

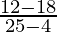
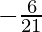
The average charge per unit of change over x = 4, 10 = 25 is -vi/21,

which is less than the derivative of y at x = 4, which we found to

be 7/3.

Question 6. Notice the instantaneous rate of alter of the given function f(x) = 2x² + 18 at 10 = nine ?

Solution:

Given: f(x) = 2x^two + eighteen

f'(ten) = 4x + 0

f'(x) = 4x

Now we have to notice the instantaneous rate of change at x = 9

f(9) = 4x

f(nine) = 4(nine)

f(9) = 36

Question seven. Find the instantaneous rate of modify of the given function f(x) = 4x² + 12x + 8 at ten = iv ?

Solution:

Given: f(x) = 4x² + 12x + 8

f'(x) = 8x + 12

Now nosotros accept to find the instantaneous charge per unit of change at x = iv

f(four) = 8x + 12

f(4) = 8(iv) + 12

f(four) = 44